A fair comparison of modern models' reasoning capabilities
The convergence of models' interfaces on the Chat Message API as well as the global push toward larger context sizes opens an interesting opportunity to compare recent models in a perfectly equivalent setup on a reasoning-heavy dataset: MATH.
Models
We present an evaluation of the following models on the MATH dataset:
- Anthropic:
claude-instant-1.2claude-2.1 - Mistral:
mistral-medium(unreleased)mistral-small(the 8x7B) - Google:
gemini-pro - OpenAI:
gpt-4-1106-previewgpt-3.5-turbo-1106
All models are aligned to follow instructions through a chat interface. All have a context size of 32k tokens or more. The interface their API present are similar, converging on the Chat Message interface introduced by OpenAI (see code).
We did not evaluate llama-2-chat because of its limited 4k context size, which would have resulted in an unfair comparison (as our methodology relies on at least ~8k context size).
Dataset
The MATH dataset consists of mathematical questions with a unique numerical response. The dataset includes for each question a reasoning as well as an answer. These exercises are at high-school Olympiad / early-undergrad Olympiad levels, making this dataset a great probe in the reasoning capabilities of models.
This dataset also comes with limitations. It is sourced from actual US Olympiad problems (AMC, AIME, ...) that are discussed online, leading to unavoidable contamination, potentially favoring larger models. Despite this intrinsic limitations it remains one of the best dataset to evaluate models reasoning capabilities.
Limitations
We use for our evaluations a random sample of 128 problems (balanced over categories and difficulty levels) from MATH test split. 128 is definitely a small number to evaluate on the MATH dataset, but the goal of this project is first and foremost to compare models, more than to compute a precise evaluation metric on MATH for each of them.
Evaluation
We evaluate using Chain-of-Thoughts (CoT) prompting with consensus. CoT prompting means that we incentive (through few-shot prompting) the model to provide an explanation (a proof here) before producing an answer. This technique is known to help models produce better answers. Consensus means that we run this process multiple times per problem (leading to a variety of responses due to models stochasticity) and pick the answer that was generated the most for each problem. For each execution within a consensus pool we sample different train set problems to use as few-shot examples to improve diversity.
The most interesting part of this project, is that the exact same messages were sent to all models, making this model comparison a "bit-wise" model comparison, only possible thanks to the recent convergence by all model providers to a unified chat-based interface and alignment process.
We use seeded random generators throughout the code to guarantee that the exact same messages were sent to all 7 models. We perform a total of 32*128=4096 queries per model to perform the evaluations. The cost of running one evaluation is approximately $50-$100 depending on each model pricing.
An example "query" can be found at the end of this blog post (Appendix A).
The evaluation code is available here: https://github.com/dust-tt/dust/tree/main/x/spolu/research/evals
Note
MATH is known for having noisy notations for the final answer generally presented using a \boxed{} LaTeX directive (eg: \boxed{frac12} vs \boxed{frac{1}{2}}), which interferes with the consensus mechanism. Instead of implementing an inevitably brittle sanitization function, we used GPT-4 to sanitize the answers of the train and test splits. The main advantage to use a model is that we can provide the same sanitization or formatting instructions to the evaluated models, significantly reducing the chance of false-negatives . The sanitized test problems can be found here.
Results
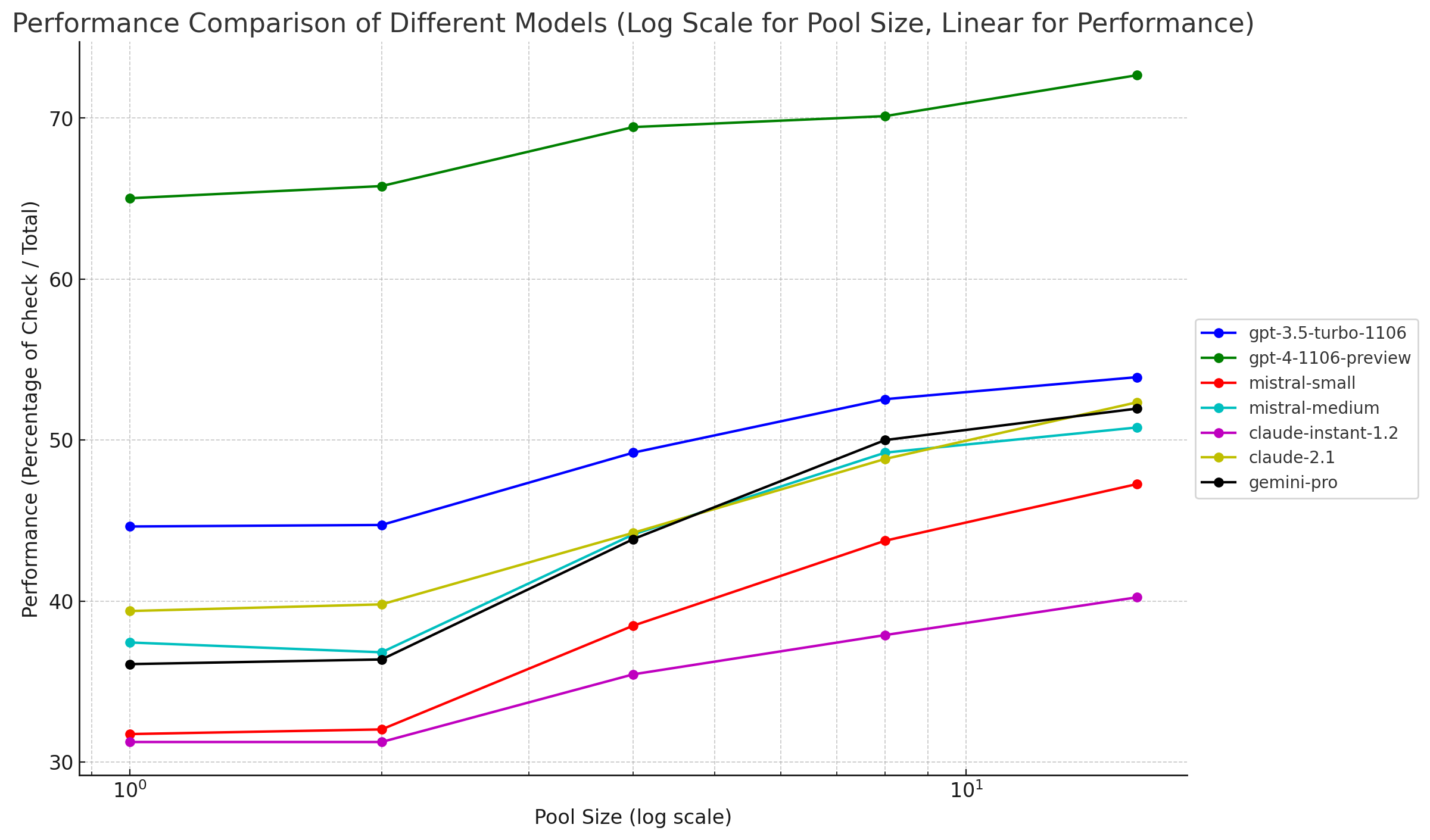
The raw results are presented in the table below. The numbers are the averaged number of successfully answered problems at each consensus pool size (out of 128 problems).
| Model | 1 | 2 | 4 | 8 | 16 | 32 |
|---|---|---|---|---|---|---|
| gpt-3.5-turbo-1106 | 57.13 | 57.25 | 63.00 | 67.25 | 69.00 | 68.00 |
| gpt-4-1106-preview | 83.22 | 84.19 | 88.88 | 89.75 | 93.00 | 95.00 |
| mistral-small | 40.63 | 41.00 | 49.25 | 56.00 | 60.50 | 62.00 |
| mistral-medium | 47.91 | 47.13 | 56.50 | 63.00 | 65.00 | 68.00 |
| claude-instant-1.2 | 40.00 | 40.00 | 45.38 | 48.50 | 51.50 | 51.00 |
| claude-2.1 | 50.41 | 50.94 | 56.63 | 62.50 | 67.00 | 65.00 |
| gemini-pro | 46.19 | 46.56 | 56.13 | 64.00 | 66.50 | 70.00 |
We run our evaluations with a pool size of 32 (this is the consensus part) which means we get pretty good estimates of the "pass-rate" (percentage of successes) for smaller pool sizes (as we can average on multiple pools) but only an bare estimate for pool size 32.
The associated pass-rates (success rates) are presented in the graph below (omitting pool size 32).

Conclusion
It is critical to our mission at Dust to keep a close eye on models' performance and how they compare. The convergence of all model providers toward larger context and the unified Chat Message interface, opened a unique opportunity to perform a "bit-wise" comparison on the MATH dataset.
The results are pretty clear. OpenAI models remain far ahead of competition when it comes to reasoning. But it is also extremely exciting to see the progress of Mistral, with mistral-medium matching claude-2.1 and gemini-pro!
Subscribe for further update on this evaluation project. We'll deep-dive in the effect of consensus, it's limitation and much more in upcoming posts.
Appendix A: Example query
+++++++++++++++++++++++++++++++
[system]
-------------------------------
<Instructions>
Find a solution to the provided mathematical problem. The answer is a unique mathematical expression presented in LaTeX `\boxed{}` directive. (example: `\boxed{4}` or `\boxed{3\pi}`). Formatting instructions: fractions should be represented in the LaTeX form `\frac{a}{b}` (not `\frac12`), units should not be included, square roots should be presented in the LaTeX form `\sqrt{c}` (not `\sqrt2`), all spaces and non critical parentheses or formatting should be stripped, rational numbers should be presented with a leading `0`.
Provide a reasoning consisting in multiple steps, using one line per step. A reasoning step is one coherent step of mathematical reasoning. It should hold in one line of at most 500 characters. If an answer is reached as part of the reasoning, it should be included in the reasoning step using the `\boxed{}` directive. Don't use the `\boxed{}` directive for anything else than the answer.
</Instructions>
<Example>
QUESTION: The average of Amy's, Ben's, and Chris's ages is 9. Four years ago, Chris was the same age as Amy is now. In 3 years, Ben's age will be $\frac{2}{3}$ of Amy's age at that time. How many years old is Chris now?
REASONING:
Let Amy's, Ben's, and Chris's ages be $a$, $b$, and $c$, respectively
We have the equation $\frac{a+b+c}{3}=9 \Rightarrow a+b+c=27$
We also have the equation $c-4=a$
And the equation $b+3=\frac{2}{3}(a+3)$
From Equation (3), we have $b=\frac{2}{3}(a+3)-3$
We substitute Equation (2) into Equation (3) to eliminate $a$, to get $b=\frac{2}{3}(c-1)-3$
Substituting this last equation and Equation (2) into Equation (1) to eliminate $a$ and $b$, we have $c-4+\frac{2}{3}(c-1)-3+c=27$
Solving for $c$, we find that $c=13$
Thus, Chris's age is $\boxed{13}$
ANSWER: \boxed{13}
</Example>
<Example>
QUESTION: What is the value of $f(-1)$ if $f(x)=x^{2}-2x$?
REASONING:
To find $f(-1)$, we substitute $x$ with $-1$ in the function $f(x)=x^{2}-2x$
$f(-1)=(-1)^{2}-2(-1)$
$(-1)^{2}-2(-1)=1+2$
$1+2=\boxed{3}$
ANSWER: \boxed{3}
</Example>
<Example>
QUESTION: What is the equation of the line parallel to $4x+2y=8$ and passing through the point $(0,1)$? Write the equation in slope-intercept form.
REASONING:
First, subtract $4x$ from both sides of the equation $4x+2y=8$ and divide by 2 to write the given line in slope-intercept form
This gives $y=-2x+4$. The slope of this line is $-2$
So, we need to find a line with a slope of $-2$ that passes through the point $(0,1)$
Writing this requirement in point-slope form gives the line $y-1=-2x$
Or equivalently, $y=-2x+1$ which is the equation of the line in slope-intercept form
ANSWER: \boxed{y=-2x+1}
</Example>
<Example>
QUESTION: Evaluate $\log_\frac{1}{3}9$.
REASONING:
Let $x = \log_{\frac{1}{3}}9$. Then, we must have $\left(\frac{1}{3}\right)^x = 9$
Since $\left(\frac{1}{3}\right)^{-2} = 9$, we find that $x = -2$
Therefore, $\log_{\frac{1}{3}}9 = \boxed{-2}$
ANSWER: \boxed{-2}
</Example>
+++++++++++++++++++++++++++++++
[user]
-------------------------------
QUESTION: What is the minimum value of $y$ if $y=3x^2+6x+9?$
+++++++++++++++++++++++++++++++
[agent]
-------------------------------
REASONING:
First, complete the square for the quadratic equation $y=3x^2+6x+9$
Rewrite the equation as $y=3(x^2+2x)+9$
To complete the square, add $(\frac{2}{2})^2=1$ after the $2x$ to get $y+3=3(x^2+2x+1)+9$
This simplifies to $y=3(x+1)^2+6$
Since $(x+1)^2\ge0$, the minimum value of $y$ occurs when the squared term is $0$
The minimum value of $y$ is $y=3(x+1)^2+6=3\cdot0+6=\boxed{6}$
ANSWER: \boxed{6}
+++++++++++++++++++++++++++++++

